Uma das partes mais mágicas da Estatística é ser capaz de fazer inferência sobre alguma característica de uma população, enxergar padrões em certos comportamentos e assim conseguir tomar as decisões de forma consciente. Por exemplo, sabemos que o algoritmo quick sort tem uma complexidade de O(\(n^2\)) quando o vetor já está ordenado. Mas será que mesmo assim vale a pena usar esse algoritmo no sistema? É comum que o algoritmo entre no pior caso, se escolhermos o pivot aleatoriamente? Ao fazer a análise de complexidade média, vemos que a complexidade mais proável seria de O(n log n).
No entanto, alguns casos de estudo não são tão previsíveis como este célebre algoritmo e nem sempre é possível fazer uma análise que englobe a totalidade dos dados. Imagine tentar descobrir as chances de um candidato ganhar uma eleição analisando toda a população ao invés de fazer inferências, como as pesquisas de intenção de voto: a coleta de dados se mostraria não só um processo extremamente custoso financeiramente como demasiado lento para uma análise onde o tempo é crucial.
Teste de hipótese
Vê-se então a utilidade da inferência estatística, que baseia-se em, a partir de uma amostra, estimar algum parâmetro (média, por exemplo) envolvendo toda a população. Entretanto, ao formular uma hipótese estatística é preciso estar de posse de algum mecanismo que ofereça certa garantia de que a dedução feita ao analisar uma pequena parte do todo também vale no mundo real.
Uma das formas de obter essa resposta é através do teste de hipótese, cujo conceito foi forjado por Ronald Fisher, considerado por alguns o pai da estatística moderna. São formuladas duas hipóteses: \(H_0\), também conhecida como hipótese nula; e \(H_1\), que recebe o nome de hipótese alternativa e preferencialmente deve ser complementar à hipótese nula. O processo consiste em testar \(H_0\), avaliando a probabilidade dos dados observados ocorrerem assumindo que a hipótese nula seja válida.
Testar uma hipótese supondo que ela é verdadeira e ainda por cima sem ter todos os dados? Parece contraditório.
Reductio ad absurdum
O argumento lógico por trás desse método é o reductio ad absurdum. Ao supor uma proposição, é desenvolvido o pensamento até que o resultado seja algo tão absurdo que invalide a suposição inicial.
Digamos que você quer provar que seu programa funciona, então essa seria sua hipótese. Intuivamente, sabemos que ele deve funcionar perfeitamente em diversas situações. Para isso, você o submete a uma bateria de testes mas observa que nem todos os casos são atentidos, encontrando uma contradição com sua premissa de que deveria rodar em todos os casos. Logo, você conclui que seu programa não está funcionando.
Para o teste de hipótese, a linha de raciocínio começa assumindo que a hipótese nula é válida. Ao analisar os dados disponíveis é obtido o parâmetro. Com base em um nível de significância, é visto o quão o parâmetro se distancia de um valor razoável de acordo com um modelo, ou seja, se esse valor seria muito raro de se obter caso a hipótese nula fosse verdade. Então, ao obter um \(\alpha\) pequeno, chegamos a uma contradição, visto que ao assumir \(H_0\) como verdadeira é esperado um nível de significância alto. Se for o caso, é bem provável que nossa tese esteja errada, e podemos dizer que a rejeitamos.
Ao utilizar a conclusão obtida pela técnica mencionada, podemos interpretar que o parâmetro ser obtido implica que \(H_1\) é válida.
O valor que usamos como limiar para definir se rejeitamos a hipótese nula é p<0.05, ou seja: a probabilidade de ocorrência dos dados analisados uma vez que a hipótese nula seja válida deve ser menor que 5%.
Fun fact: o valor padrão de significância para um p-valor, p<0.05, foi apenas uma definição arbitrária do próprio Fisher em uma de suas publicações (que veio a ser adotado por toda a comunidade científica), desprovido de qualquer justificativa objetiva.
Atribuindo valor às variáveis
Enumerados os termos usados, um exemplo ajuda a visualizar melhor como esses dois conhecimentos se misturam.
Digamos que nós queremos estudar o comportamento de acessos a um site que uma certa equipe é responsável. Depois de algum tempo, com base no retorno obtido das redes sociais, um dos integrantes acha que o percentual de usuário que possuem graduação é em média 60%, com 10 % de desvio padrão. Alguém da mesma equipe discorda, achando que a proporção deve ser diferente.
Para saber quem está mais próximo do resultado real, façamos com que \(H_0\) represente a hipótese de que em média o percentual dos usuários que acessam o sistema possuem graduação seja diferente de 60% e \(H_1\), a afirmação que o percentual médio é igual a 60%.
Existem dois modos de verificar se a hipótese nula deve ser rejeitada, depois de escolhido o nível de significância \(\alpha\), que geralmente é em torno de 0,05 e 0,1. Uma é usando p-valor, onde o p-valor menor que o nível de significância implica em rejeitar \(H_0\). Outra é calculando a região crítica, ou regra de decisão, que define um intervalo para o parâmetro \(\bar X\), no qual \(H_0\) será rejeitado. Ao calcular o parâmetro, é testado ele está contido na região crítica e, se for o caso, a tese é rejeitada.
Vamos supor que ao fazer uma simulação dos usuários, foi obtido o histograma abaixo e que ao calcular o p-valor, seu valor é de 0.03:
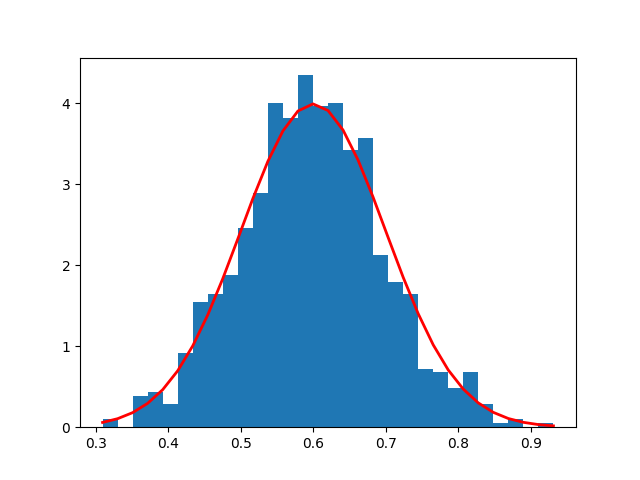
Neste caso, \(H_0\) é rejeitado, ou seja, podemos dizer que há evidências de que o percentual médio dos usuários que acessam o sistema possuem graduação é 60%.
Links
Aula do Khan Academy sobre testes de significância
Discussão sobre reductio ad absurdum e prova por contradição
Vídeo-aula sobre teste de hipótese do Crash Course Statistics
Estratégias de demonstração em Dedução Natural
Twitter Facebook